The Lines are Not Always Parallel! A geogebra approach to Alternate Interior Angles
 Students are frequently confused by us harping on the importance of things that seem obvious: because we hardly ever show them the cases where the theorems are false. One of the areas this comes up is Angles in Parallel Lines. (The whole course of Geometry may feel like this, actually). We teachers might feel like, “how do kids get confused here? its so easy and obvious!” That’s right… so easy and obvious that we teachers have lost sight that we only show them these narrow cases.
Students are frequently confused by us harping on the importance of things that seem obvious: because we hardly ever show them the cases where the theorems are false. One of the areas this comes up is Angles in Parallel Lines. (The whole course of Geometry may feel like this, actually). We teachers might feel like, “how do kids get confused here? its so easy and obvious!” That’s right… so easy and obvious that we teachers have lost sight that we only show them these narrow cases.
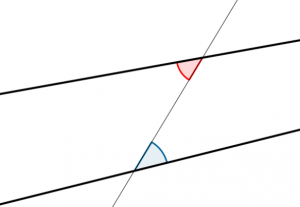
We spend time proving that certain pairs of angles on parallel lines are congruent or supplementary. Over and over and over… but always parallel lines!! Maybe maybe we make an offhand comment about “if these lines weren’t parallel then the angles wouldn’t be congruent!”. But those words hardly paint the picture for student.
But think of the infinite number of line that are not parallel!!
![]() So, let us turn to Geogebra. My philosophy in making this applet (and most of my applets) is to loosen some restrictions in our normal presentation so that more of the “sample space” can be explored. Lets consider all lines cut by a transversal, not just parallel lines. Then how many students will not only (1) appreciate parallel’s special nature and (2) make conjectures about congruent angles all by themselves? This is much in the same vein as Michael Serra‘s Discovering Geometry book: set up a situation so that the students actions will lead them to make those conjectures.
So, let us turn to Geogebra. My philosophy in making this applet (and most of my applets) is to loosen some restrictions in our normal presentation so that more of the “sample space” can be explored. Lets consider all lines cut by a transversal, not just parallel lines. Then how many students will not only (1) appreciate parallel’s special nature and (2) make conjectures about congruent angles all by themselves? This is much in the same vein as Michael Serra‘s Discovering Geometry book: set up a situation so that the students actions will lead them to make those conjectures.
The applet here lets students drag the line to all positions, and illustrates the red and blue angles, giving no measurements. We want intuition here, not measurement. Students might already have some idea “yeah they look close enough”.
The check box “Compare Angles” allows them to update their intuition when faced with a little more precision. This kid who wasn’t able to articulate anything before might now realize in what realm we are trying to explore.
The check box “Compare Lines” allows them to make a connection to the properties of the pairs of lines. Again, this is some non-verbal feedback and prodding to a student. The student must assimilate this and then can provide the verbalization themselves.
Finally, I added in a little game at the end. It will spit out a score based on how close to congruent the angles are. (The formula is arbitrary, but spikes up very high when you’re close). Let me know how this plays out with your students! Do they get invested in beating each other’s high scores? If so, notice that in trying to beat one-another, they must know that they want to make the lines “more parallel”. Here we can embrace the difficulty of being precise when doing this with a trackpad or touchscreen. Will your students say “hey if I could make them parallel, that should be an unbeatable perfect score!” (I actually think Geogebra will spit out “infinity” score if it gets close enough– a happy consequence of the data structures they’re using)

Big fan of the premises here, Scott.