Student Inquiry into the Neighborhood of the Special Case
Lets look at Triangle Centers: a fun unit for many Geometry classes. Its a topic with some good “real-world” applications, certainly, but we need not always justify our lessons with application. And it may hold us back from important mathematical practices. Pure math is underrated! Lets compare some traditional textbook style application problems with an interactive style problem. First, Holt Geometry:

 Those two problems are somewhat typical of some application motivators. But consider a correct response from a student:
Those two problems are somewhat typical of some application motivators. But consider a correct response from a student:
18. Main street should be the angle bisector of the angle between Elm Street and Grove Street.
37. Bisect the angle between the streets. Draw the perpendicular bisector between the museum and the library. The visitors center should be where those two lines cross.
How does this capture the imagination of a student? If they know what an angle bisector is, they can supply an answer. But if they do not know it (or haven’t made the connection about equidistance from sides) what kind of feedback can you give them that guides them to the answer without providing the answer?
But the book already provided the direct answer, earlier in this section: Theorem: a point is on the bisector of an angle if and only if it is equidistant from the sides. #18 is almost explicitly asking for this theorem. #37 asks a little more: it wants this theorem combined with the perpendicular bisector theorem, which led off this section– no prelude. These questions are merely dressed up versions of those on Level 1 and Level 2 of Bloom’s Taxonomy.
With GeoGebra, we can provide loads and loads of information that (1) helps guide the student around the topic we want and (2) does not provide progress towards “the answer” in discrete unassailable steps. We can be more helpful while being #lesshelpful.
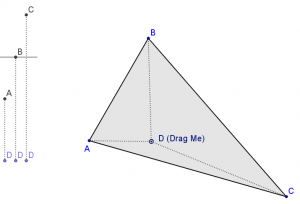 Here is a picture of an applet I created to give some real-time information to students about point D and triangle ABC. And here is the interactive applet itself, try it!
Here is a picture of an applet I created to give some real-time information to students about point D and triangle ABC. And here is the interactive applet itself, try it!
In this first static picture, what information is given to students? Most students will be keen enough to see the comparison of the distances DA, DB, DC. And all students will catch on after they start dragging point D.
What do we need to ask here to get students to think about perpendicular bisectors? I say: “not much!” My introduction to the applet is “Drag point D. Find special locations.” That’s not to say I’m not communicating with the students. I’m communicating a great deal more! I’m communicating through the boundaries and feedback programmed into the Geogebra manipulative. Manipulatives are powerful in any setting, but computerized manipulatives enable modes of lessons not possible before.
I love doing triangle center lessons via oragami (or patty) paper. I love doing triangle center lessons via compass and straightedge. But the boundaries of those manipulatives do not guide the students. If you make an incorrect fold or line, the paper doesn’t tell you so. If you want to test distances with your compass or ruler, you must do them one at a time. If you want to pursue a question other than equidistance (e.g.) then there may be other complicated procedures to follow.
Consider with GeoGebra: by restricting the interaction to only dragging D, the students may no longer make unproductive moves. Every move they make produces feedback via the distance “bar graph” and the color shading of D itself. That feedback isn’t telling the student “incorrect”. It is telling the student “here are the distances your input asked for.” The student is then left to parse that information, and respond with more input. This type of interaction between student and computer occurs within a fraction of a second. And this type of interaction is repeated tens, hundreds, or thousands of times. The student can then use the information to start digging into the prompt: what are the special locations for D? What makes a location special anyway? These are questions that can be asked and answered by students without teacher interruption.
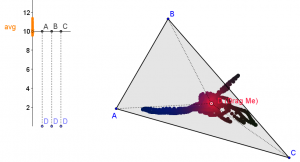 But wait, there’s more! Lets say a student has decided upon finding the place where DA=DB=DC. Computerized Manipulatives now allow a task between this decision and the answer. They must spend time actually getting point D to the correct spot. In this Geogebra applet, they have the feedback from color and the bar graph to help them, but here is where the teacher can wait for a student to ask, “is there a better way?” Boom! We have arrived at the motivation for the circumcenter construction. This motivation was driven by “pure” math ideas like equidistance… only we didn’t have to say it. Proof in geometry should be introduced as a way to perfect our conjectures and hypotheses. If the students haven’t made a conjecture, how are they going to care about its truth?
But wait, there’s more! Lets say a student has decided upon finding the place where DA=DB=DC. Computerized Manipulatives now allow a task between this decision and the answer. They must spend time actually getting point D to the correct spot. In this Geogebra applet, they have the feedback from color and the bar graph to help them, but here is where the teacher can wait for a student to ask, “is there a better way?” Boom! We have arrived at the motivation for the circumcenter construction. This motivation was driven by “pure” math ideas like equidistance… only we didn’t have to say it. Proof in geometry should be introduced as a way to perfect our conjectures and hypotheses. If the students haven’t made a conjecture, how are they going to care about its truth?
In this applet I decided to include an extension: another triangle center. But this is not the usual 2nd center introduced. Your students will find the blue point and notice what is special. Try it yourself! Think about what is also done with this wordless separation of the two points in contrast to a lecture-based introduction: the students will have their own vocabulary to parse the difference that they have played with already, instead of the students having to parse vocabulary that describes a difference that they may not have been aware of.
In this applet I included two “answer” checkboxes. Depending on where you want to take your class next, it they may steal some thunder from the lesson, but I figured I’d include them to help illustrate the point… and points. (hah)
GeoGebra and other computerized manipulatives enable us to think about Geometry and math in a way unfamiliar from static text or lecture. Similar to The Lines Are Not Always Parallel, I’ve created a way for students to observe the neighborhood around the special case, and constructed silent helpful barriers and footholds that students can grab onto as they discover what is special for themselves.
Let me know what you think.
