Comments from other sites: Four animated gifs of the same awesome problem (dy/dan)
CFOS: Comments from other sites: I do a pretty good amount of writing online about math and math ed… just its not always here. In these posts I will link to the other site and copy over my comment with some context if needed. Mostly this is for me, so that I have a journal of what my thoughts were kept in one place.
Today’s CFOS is from Dan Meyer’s blog regarding the wonderful and somewhat famous task posed by Malcom Swan. Dan writes,
Here is the original Malcolm Swan task, which I love:
Draw a shape on squared paper and plot a point to show its perimeter and area. Which points on the grid represent squares, rectangles, etc? Draw a shape that may be represented by the point (4, 12) or (12, 4). Find all the “impossible” points.
We could talk about adding a context here, but a change of that magnitude would prevent a precise conversation about pedagogy. It’d be like comparing tigers to penguins. We’d learn some high-level differences between quadripeds and bipeds, but comparing tigers to lions, jaguars, and cheetahs gets us down into the details. That’s where I’d like to be with this discussion.
So look at these four representations of the task. What features of the math do they reveal and conceal? What are their advantages and disadvantages?
paper

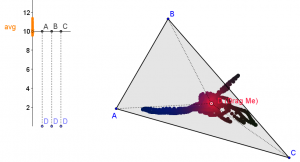
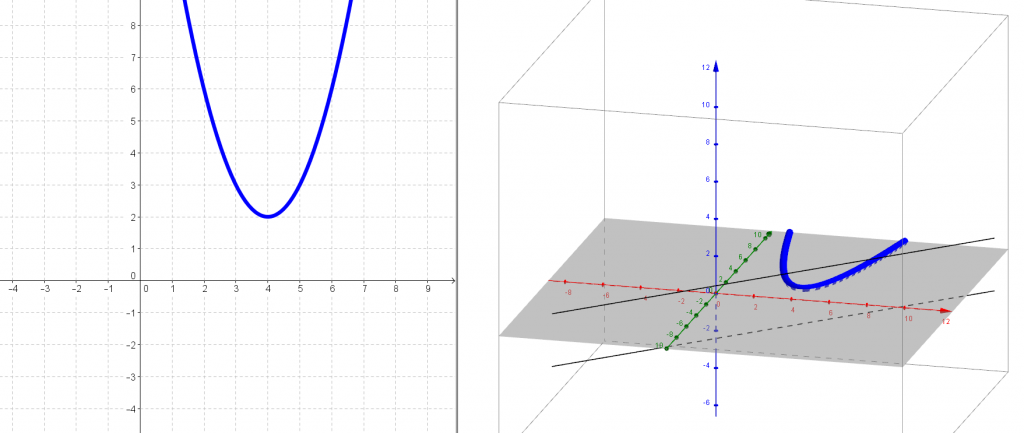
processing (code from Dan Anderson)

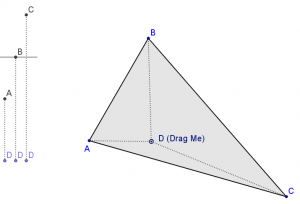
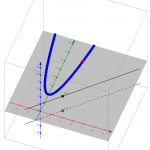
Geogebra by Scott Farrar

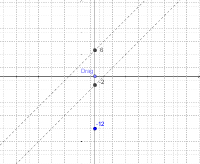
Desmos activity by Dan’s twitter followers

And my comments:
I’d love a combination of all of the above.
It appears that the Desmos activity had a drawback of no error checking. (Or, to call back your talk at CMC Asilomar, if this were a video game it would ask you to try again if your perim/area were impossible) In a customized Desmos applet, could you ask for width and height during the brainstorm rectangle phase, and then the second screen asks for perim and area? (couple more options here… you could still accept perim and area that do not match the given width, height: just flag them separately and then you can filter them out of the overlay or include them depending on where you want to take the lesson next)
It also appears that someone was investigating rectangles of a certain type, thus creating a rather straight line. Nice conversation starter there…
I think I am partial to the ability of my geogebra one to have the non-numerical entry point. On the other hand, they aren’t directly improving their skills in that arena either. A student is not hindered by calculation, but neither are they supported in it. But… I have liked giving a task to students where their interaction is manual and analog– meaning they are digging into the constraints and boundaries of a mathematical concept by physical motion and visual feedback. Does a student become immediately aware of and curious about this region that they cannot seem to get the dots into?
The processing one I like as a contrast to the hand-implemented geogebra. How would we systematically experiment around this idea? And when we devise a systematic approach, computers can be helpful in executing it. We can see the density of the dots is not uniform — what is the interaction between this perim v. area relationship and the way we have implemented our experiment? (I would guess the rectangle dimensions are chosen at random, thus creating a would-be-uniform display if not for the fundamental perimeter-area idea.)
The hand graph is limited in iteration, prone to calculation error, and slow. However, its requirements are all internal (save paper and pencil) rather than computer-based. Graphing by hand is perhaps the handle onto all of these other ideas. Is there research around how the concept of cartesian graphing changes if we grow up experiencing it in the computerized sense without the pencil and paper sense? I wonder!
For now I’d love to mix all of these in the classroom. When I spoke about this problem at Asilomar 2013, I used Malcom Swan’s initial prompts and provided grid paper for the attendees to grapple with the problem. Only afterwards did I move to the geogebra version (2013 version here, that has a slightly different scope)
And I would start the same way with students now. Here’s a rough timeline for a 1-2 day lesson:
1. paper rectangle in groups. Make a Perim v. Area graph on paper in your group that has your four rectangles. (this may correct some errors right away, like if kids put width and height instead of perim/area, their group may correct them)
2. Groups share on Desmos, add more rectangles. They are released from having to graph them on paper now. We are letting that go because Desmos will pick it up. Thus allowing students to step up their conceptual / abstracted approach.
3. class discussion, noticings, wonderings, address errors… blank region may become clearly curious here. Ok, now we’ve used the Desmos tool, but if we want to dig in with more rectangles, lets switch tools.
4. Geogebra sketch and/or programmed iteration. Groups come up with things to try and experiment with on the geogebra sketch, or devise a script that would generate perims and areas and plot them like Dan Anderson’s.
5. Return of the single case. Which points are on the edge? Can investigate with Geogebra sketch by hand. Or: can hand the class a mission on Desmos: “come up with rectangles that you think are on the edge”.
6. depending on the level of the class you can lead this towards some kind of proof or justification, entice students to make reasoned conjectures about what is going on.
Now we’ve taken the stepping stones from drawing a single rectangle to an aggregate set of many rectangles and their (p,a), to a set larger than what we could human-ly create. When we’re on step 4 there, we’re getting a handle on the abstraction of perimeters and areas of rectangles, thus allowing us to experiment with the abstraction just as easily as we worked with a single rectangle on paper at the beginning of class. But then we can go back and use each tool for what it helps with.
That, I believe, is the power of education technology: giving concrete handholds to abstract concepts. But tech is at its most powerful when working in concert with non-tech methods. And the possibilities of tech are so wide that no single tool was the magic bullet that enables this lesson– each one exposed a new vector to take.
Finally, remember Swan’s prompts (that did not aim to use technology) originally got at the existence of this concept by suggesting an impossible point and then suggesting that there are many others to find. His prompt defines these two regions (that we might call white and red for our purposes) with two examples: one red and one white. I wonder what the difference is about investigating the existence of white and red by imagining and reasoning on paper vs. bouncing up against their boundary on the geogebra applet.


 Those two problems are somewhat typical of some application motivators. But consider a correct response from a student:
Those two problems are somewhat typical of some application motivators. But consider a correct response from a student: