Treating the virus 8 ÷ 2 (2 + 2)
Recently, another instance of an arithmetic problem went viral. As math teachers, we might get asked our professional opinion and I think some of us are getting frustrated:
Or maybe many of us? (nytimes)
8 ÷ 2 (2 + 2)
People argue over the answer being 1 or 16, since it’s unclear which order to perform the operations. If truly faced with this, we’d ask what the person meant, perhaps lightly scold them for writing ambiguously.
Dan said we should be horrified. It presents an image of math as symbolic manipulation, or numerical calculation. Or worse: math as a place where there is only one correct way to do things.
I don’t disagree entirely, but we have to acknowledge the virality as evidence that this is where people are in their understanding of math. It interests them on some level, at least at the level that they are confident in their own answer enough to seek validation or comparison with others.
If we want to move people forward, like we would any student, we meet them where they are and help them take their next step.
Virality not guaranteed, but I wondered what might interest someone who has delved into the initial problem. Could we find a problem just tantalizing enough to lead them towards more interesting mathematics? (What’s this tweeter’s ZPD?)
I took a quick stab at two followup questions:
- How many answers are there?
8 ÷ 2 ÷ 2 ÷ 2 - What numbers can go in the blanks so that all the answers are integers?
24 ÷ [ ] ÷ [ ] ÷ [ ]
Or in image format:
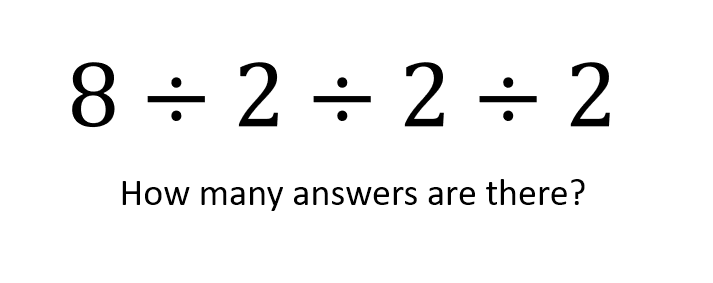
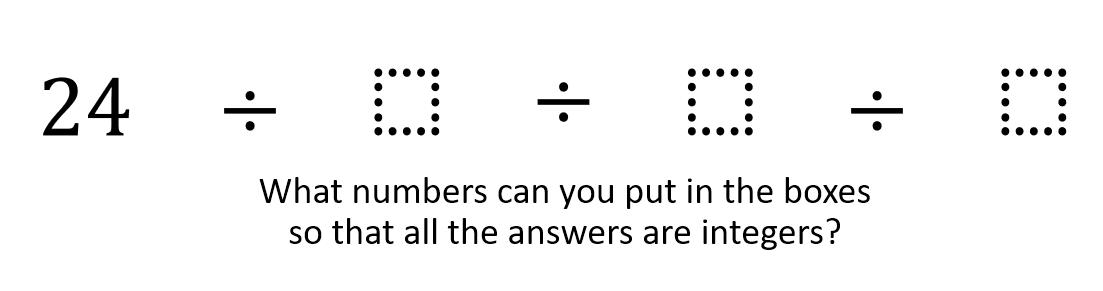
Shoutout to https://www.openmiddle.com/ for the format of the second question.
The first one is intended to lead from the viral question towards a solid belief that this style of writing produces multiple answers. Well– how many?
The second question turns out to be pretty juicy. You could find some easy numbers to make it work, but can you challenge yourself to find more? How many are there? How do you know? I also think it’s interesting how the ambiguity we learned about the division operator helps us concisely communicate this problem.
We can argue about 1 or 16. We can argue that we shouldn’t have to argue about 1 and 16. But I’d rather take those infected by order-of-operations virality as an opportunity to take them someplace interesting.
