Efficient Grading in Four Easy* Steps
Recently, Michael Fenton (@mjfenton) posed the following question:
Q4 What advice would you give to a younger version of your teaching self regarding grading? #slowmathchat pic.twitter.com/E9yw2SFemT
— Michael Fenton (@mjfenton) February 27, 2015
I thought back to the types of grading I was doing in my first few years of teaching. I would go through problems with a fine-toothed comb, taking points off the maximum… minus one here, minus two there… minus 1.5 point here, because “I can tell you know it, but you forgot a negative sign a couple steps ago, and as we all know, negatives signs are worth half a point”. I would make sure all my tests had appropriate weights on each question, “number 2 is worth 5 points, and number 3 is worth 7 points” (because it’s 140% harder!) and I made sure to write very encouraging comments or constructive criticism that I’m sure contained very little mistakenly copied dialogue from the CSI episode I was watching. “Jimmy, you have a good idea here when you divide the perimeter by two, but did you gather the DNA sample from the suspect?” And of course, my gradebook followed precise weights and scales: “yes, 30% tests, 15% quizzes… because if I say the word test I want to make sure you stress exactly twice as much over each problem– also you have less time.”
It was exhausting. And with more experience I was beginning to see where the extra work came from, such as evaluating the worth of assignments, problems, and categories of problems– a task that required extreme time and effort to nudge the system way from seemingly arbitrary. Finally, I thought about what students were gaining from all of my extra work– I concluded, “not much.”
If this sounds like you, I offer these steps, in increasing levels of difficulty, to make your grading more efficient. These are things I gradually adopted over a couple years. The steps are simple, but the effects transform your teaching itself.
- All integer points.
- All problems on the same scale.
- Skip comments. *
- (we’ll get to #4 a little later)
Lets talk them through. We’ll see how they tie together and how they alter the culture of the classroom.
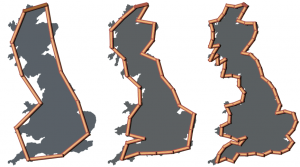 1. Stop giving fractional points. And further, reduce the total possible point outputs. Your teacher brain is expending calculation energy dealing with fractional points or a wide range of possible scores. Why? Because you want to summarize that the student has the concept but has missed some details. What message does this send? “I am somewhat ok with you being not attending to precision” ? (CCSS.MP6) Because you want to be completely sure about the value of this student’s work? Grading is a loss of information, we boil down a student’s work into a numerical value, an irreversible process, and an imperfect science anyway. Do you know what an 8 point score looks like in comparison to an 8.5 point score? Or even 8 points vs. 9 points? (out of 10, lets say) This is like the coastline paradox: you can spend a great deal more energy to find a measure that may be only slightly more useful– or may be less useful even. Does it make sense to measure the coastline of England on a scale that is affected by the tides? And are they missing half points a lot? If so– maybe its not so minor a problem. If not– then what difference will one half point make in the end? Now I’m not saying to round it all down. Where you go from what you might previously have given an 8.5 will depend on other factors. This step can be adopted by itself, you just have to decide how important those tiny errors are to the overall measure of the student’s work. You’ll save a lot of energy on your end that can be applied to other areas, and you’ll lose only a little more information than what you previously had.
1. Stop giving fractional points. And further, reduce the total possible point outputs. Your teacher brain is expending calculation energy dealing with fractional points or a wide range of possible scores. Why? Because you want to summarize that the student has the concept but has missed some details. What message does this send? “I am somewhat ok with you being not attending to precision” ? (CCSS.MP6) Because you want to be completely sure about the value of this student’s work? Grading is a loss of information, we boil down a student’s work into a numerical value, an irreversible process, and an imperfect science anyway. Do you know what an 8 point score looks like in comparison to an 8.5 point score? Or even 8 points vs. 9 points? (out of 10, lets say) This is like the coastline paradox: you can spend a great deal more energy to find a measure that may be only slightly more useful– or may be less useful even. Does it make sense to measure the coastline of England on a scale that is affected by the tides? And are they missing half points a lot? If so– maybe its not so minor a problem. If not– then what difference will one half point make in the end? Now I’m not saying to round it all down. Where you go from what you might previously have given an 8.5 will depend on other factors. This step can be adopted by itself, you just have to decide how important those tiny errors are to the overall measure of the student’s work. You’ll save a lot of energy on your end that can be applied to other areas, and you’ll lose only a little more information than what you previously had.
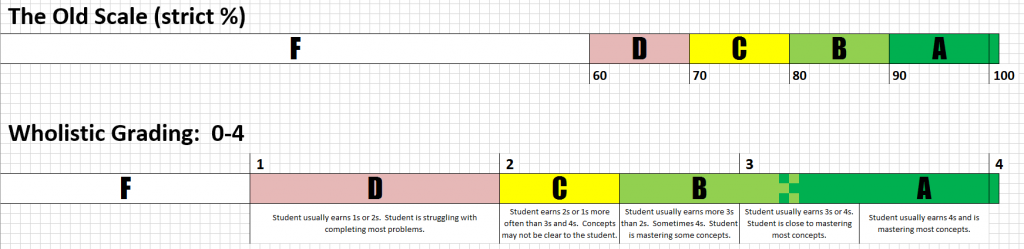
2. Put all problems on the same scale. Now that we have no fractional points, lets simplify our life even more: no more deciding what a problem is worth. No 3 point problems, no 12 point problems, no 11 point problems. Let us have all problems worth an equal amount with a small number of divisions. Now, let us also define a “problem” as something that requires work and reasoning to be shown. This can vary depending on the course, but in general, a problem is not multiple choice, or fact recall, or calculation-only.
What do we want to communicate to the student? We shouldn’t detail what is wrong or incomplete, that should be a skill practiced by the students themselves. So what do the students need in order to practice that skill? They only need to know if their work is insufficient. So to that end, I grade every problem on a very simple rubric: 4, 3, 2, 1, 0. These numbers communicate to the students the following ideas:
4: Full detailed solution
3: minor revisions needed
2: major revisions needed
1: a mathematical effort in the right direction
0: blank or no mathematical effort
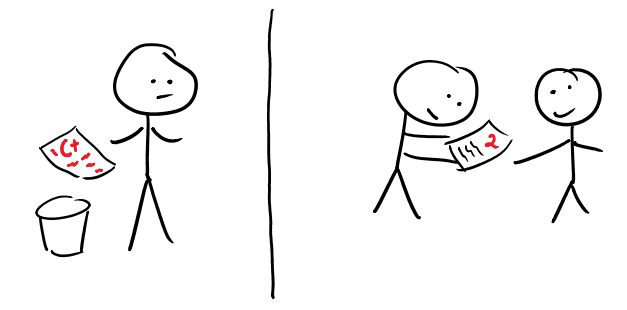
The main idea here is that we want to communicate that the student’s work can be improved. And that if they were to make revisions, it could be re-evaluated and their grade could improve. I based my structure on ideas I heard from Dr. Kysh at SFSU during my credentialing program, Riley Lark (now of ActivGrade), and Richard and Rebecca DuFour. See more comments from Riley here: http://larkolicio.us/blog/?p=800. The DuFours argument was specifically about late work– why not accept it? “Hey you didn’t pay your electric bill on time last month– so just forget about it!” This idea of revising work means that the assignments that you give are automatically more meaningful. The student remains accountable for their work after they turn it in and they are tasked to figure out how to improve it. That’s a valuable skill! And it relates to another Mathematical Practice standard: CCSS.MP3 critique the reasoning of others. Peers can help each other figure out what is lacking in their work, and what can be improved.
A quick note about scaling: the familiar 90-80-70 scale has a built in pressure towards “completionist” grading. It assumes that you will be averaging. It assumes that students will “complete” “50%” of their “work” (feel free to do air quotes along with me) before its even close to being acceptable. What does it mean to know 70% about solving equations? What is the difference between knowing 25% and 50% about triangle congruency? I thought carefully about what is being measured and what was being communicated by those numbers. I decided to jump to another arbitrary scale– the GPA scale– that corresponds better to the rubric messages I was sending. (A single 1/4 no longer drags an entire average down like a single 25% does.)
3. Skip comments. (* 2016-03-19 For additional context on this, and perhaps differing opinions / additional options, see Dylan Wiliam on Feedback)
If your problems are all on the same scale, and that scale has a versatile rubric… what comments do you need to write? Here are typical comments I used to write:
“Good idea! What if you apply that here?”
“I like this, but you can’t always do that step because …”
Sure, ideally we could devote unlimited attention towards a single student and use various pedagogy to improve their work. But we have 150 students. Time you spend on one student is time you are taking from the others. What did my comments achieve above? Was it worth the time I spent on them? Did the students internalize it? I do think there is a benefit for personally coaching or cheerleading and encouraging students, but is it a good use of time to handwrite?
Here’s what I started doing instead:
- I would score using the holistic 43210 rubric. “How good is their solution?” But that wouldn’t be the only marks on the page. I might circle things to guide their attention, or put happy faces or stars as shorthand approvals/encouragements.
- I would make notes of “interesting mistakes” ala My Favorite No, and use them as information to structure future lessons. Because, if one kid has a misconception… how many others share it?
- I carved out class time for students to work on revisions. This could be structured individually, or peer-review, or office-hours-style, or whole-class error analysis… or some mixture of those styles.
A student who reads comments may gain a lot from them. But what are they supposed to do? Wait until the mythical “next time” to address the concerns you wrote? Comments written on a “dead” assignment are asking to be thrown away and forgotten. But if you give students the expectation of revisions, then all you must do is indicate what must be revised. The assignment lives on!
This cut my grading time down by at least half. But also it served as a formative assessment of the class progress, allowing me to still make comments– but this time it was in person, to multiple students at once, and with the structured intent of them figuring out what was wrong.
Revision days sound like they will eat into your classtime, but instead they remove the need for “review/reteach days”. Plus, the students get the extra practice with critiquing and analyzing work. PLUS the grading is much less time consuming on the teacher side. PLUUUSSS it encourages culture in your class centered around improvement, growth mindset, and increases the value of every assignment you give.
4. Ok what’s step 4? Standards Based Grading. This one is a doozy. To switch completely towards assessing student’s understanding, rather than compliance, you can switch to SBG. This is an entirely new way to grade, as it requires identifying what standards are being assessed when, and how you are going to decide what kind of scores mean what kind of mastery. It also requires holding the line against some external pressure: the principal and the parents and the students themselves may resist the new style. But with the previous steps 1,2,3 above, you can be halfway there and then feel out how to make the final leap. There are various blogs about how to adjust, (I like Sam Shah) and various software to help support you (check out JupiterGrades and/or ActivGrade)
What you’ll find if you head down this road is that you begin by re-thinking what you actually want to assess… and you end by re-thinking how your assignments even work! First you think, why even grade a drill worksheet of linear equations? Then you think, what type of assignment will give the students opportunities to vary strategies and produce interesting responses to analyze in revision?
Let me know what you think… Let me know if you have similar or contributing ideas… And definitely let me know if you try it!