#ContinuumMath – join the movement!
I’m starting a new movement. Maybe its not new– and in that case I’m grabbing a banner and rallying the movement!
All too often we talk only about special cases in the math classroom. All of our teaching revolves around pointing out landmarks and marvels. But how can our students appreciate such phenomena if their experience never includes the cases that are not marvelous? If you live your whole life in Yosemite, how would you know how special it is?
That is my thought behind #ContinuumMath. We need to shake up the special cases by spreading student experiences to include the countless non-special cases.
- Going to talk about SSS or SAS triangle congruency? Why not talk about “SS” ? Why are we always using 3 parts of a triangle? I myself prefer “SASASA” congruency.
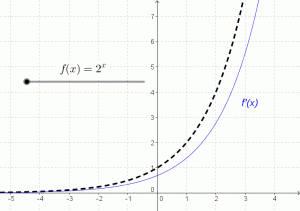
- The natural exponential function
can be explored in the context of all of the other exponentials whose derivatives are merely proportional instead of equal to their output values.
- I’ve previously discussed that lines are not always parallel. Corresponding and Alternate Interior angles are not very interesting if our “desire for congruence” is always fulfilled.
- Algebra:
. “2 step equation”? Heck, I can solve that equation in 7 steps! How about this: Students… try using 5 properties of equality (“steps”) for this equation to get to x=6 — I bet you’ll use at least one additive inverse and at least one multiplicative inverse. The inverse properties come out naturally as the most efficient moves.
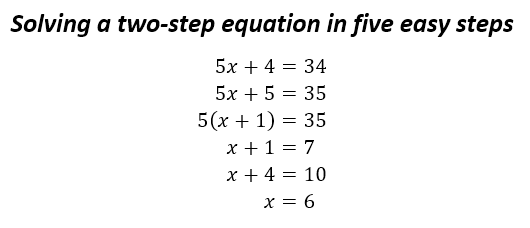
 We have lots of new technology to assist us in exploring whats around the special case. Constructing equidistant points with a compass and straightedge is what can be done after we experience [GGB] how distances change.
We have lots of new technology to assist us in exploring whats around the special case. Constructing equidistant points with a compass and straightedge is what can be done after we experience [GGB] how distances change.
Students who experience all of these non-special cases then see the special cases as actually special.
Every time your textbook or curriculum offers up a wonderful case– they’re just begging to be shaken up and explored in the context of the structures they depend upon. This is the Gift of Sometimes True. Whenever we are giving a theorem or an if-then statement, we can parameterize the condition. Here’s what I mean:
The diagonals of a parallelogram bisect each other.
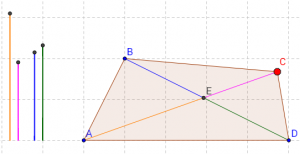 We can take that and say, the diagonals of a quadrilateral bisect each other if the quadrilateral is a parallelogram. And now we want to consider the entire continuum of quadrilaterals– I want students to see quadrilaterals that are almost parallelograms, quadrilaterals that are nowhere near parallelograms, and everything in between! We further get to talk, as a bonus, about all of the properties of diagonals in other quadrilaterals. Try the geogebra applet for yourself.
We can take that and say, the diagonals of a quadrilateral bisect each other if the quadrilateral is a parallelogram. And now we want to consider the entire continuum of quadrilaterals– I want students to see quadrilaterals that are almost parallelograms, quadrilaterals that are nowhere near parallelograms, and everything in between! We further get to talk, as a bonus, about all of the properties of diagonals in other quadrilaterals. Try the geogebra applet for yourself.
In this applet I parameterized the quadrilatral, but not fully: its impossible to get a rectangle or rhombus here– a tradeoff I made for simplicity of interaction: you can only drag point C. But as students drag, they observe the diagonals and their dissected lengths. They can make observations and comparisons in real-time, and they can conjecture and posit as they experience and interact the structure of the geometry. Students will find the parallelogram. Students will find the trapezoid. Students will also find locations where three segments are equal. Students will find quads that contain isosceles triangles formed by their diagonals… Students will discover so much more because they are seeing so much more than the narrowness of the special case. Embrace the Continuum.
Check out #ContinuumMath on twitter and/or leave replies here.