Quickie Lesson Description: Zombies and Capped Exponential Growth
I saw Julie Reulbach use Zombies to explore exponential growth and lead into logarithms. I really liked Julie’s use of the situation to prompt the need for logarithms.
It reminded me of a similar lesson I did when one year I got ambitious and dug into logistic growth as a context to exponential growth in a pre-calc class. It went pretty well but the next time I do this I’d want to incorporate some of Julie’s ideas as well…
My introduction was similar to Julie’s introduction: Zombies are attacking the class. But I decided to act it out a little bit to come to terms with the “reality” (hah) of a zombie attack. Namely, exponential growth might overestimate the infection rate since when there are already a lot of zombies, its hard to find normal healthy humans to devour their brains.
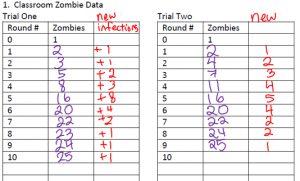 So we acted out a slightly different model: I asked for a student volunteer to be “Patient Zero” and had them come up to the smart board to run the random number generator (“RNG”) from 1-32 (my students each have a number according to the alphabetical roll sheet, it comes in handy a lot). Whomever’s number got picked was then “bitten” by Patient Zero and now there were two numbers. The next round, each zombie would roll the RNG and bite a classmate (lots of great acting going on here…) with one caveat: if the RNG came up with someone who was already a zombie, then nothing happened. The students called this situation a “dumb zombie” event. What this meant was that we would start with exponential doubling, but the more zombies there were, the less likely we’d get new zombies, because we were near the “food” supply cap– similar to a predator/prey population model.
So we acted out a slightly different model: I asked for a student volunteer to be “Patient Zero” and had them come up to the smart board to run the random number generator (“RNG”) from 1-32 (my students each have a number according to the alphabetical roll sheet, it comes in handy a lot). Whomever’s number got picked was then “bitten” by Patient Zero and now there were two numbers. The next round, each zombie would roll the RNG and bite a classmate (lots of great acting going on here…) with one caveat: if the RNG came up with someone who was already a zombie, then nothing happened. The students called this situation a “dumb zombie” event. What this meant was that we would start with exponential doubling, but the more zombies there were, the less likely we’d get new zombies, because we were near the “food” supply cap– similar to a predator/prey population model.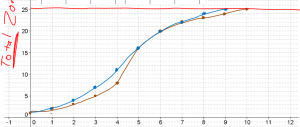 It really served to de-emphasize the “single correct predictive model” idea. We had the tools of exponential growth which kind of helped describe our situation, but if we consider the logistic model as well, it helps us fix some of the imperfections. And of course, the logistic model is no guarantee to be perfect either. We had a good class discussion around how each model incorporates some variables (in the general sense) and assumptions while neither may capture the whole picture. I also asked, “if we were to expand this to a larger population (such as the whole school), what features of the models would change or stay the same?”
It really served to de-emphasize the “single correct predictive model” idea. We had the tools of exponential growth which kind of helped describe our situation, but if we consider the logistic model as well, it helps us fix some of the imperfections. And of course, the logistic model is no guarantee to be perfect either. We had a good class discussion around how each model incorporates some variables (in the general sense) and assumptions while neither may capture the whole picture. I also asked, “if we were to expand this to a larger population (such as the whole school), what features of the models would change or stay the same?”
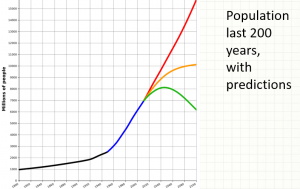 Finally, I wrapped up the discussion by pulling up some population graphs for human civilization. Noted that we don’t know where the supply caps are, or which caps might be solved in the future (such as how the development of agriculture allowed new growth, or more recently, how antibiotics allowed new growth). I felt this was a nice attempt to connect my math classroom to other subjects such as history (ka-ching, that rare humanities connection) and biology.
Finally, I wrapped up the discussion by pulling up some population graphs for human civilization. Noted that we don’t know where the supply caps are, or which caps might be solved in the future (such as how the development of agriculture allowed new growth, or more recently, how antibiotics allowed new growth). I felt this was a nice attempt to connect my math classroom to other subjects such as history (ka-ching, that rare humanities connection) and biology.
You can see my slides from this lesson here: ma 2013-03-15 They don’t have everything, (because I try to use the smartboard + a whiteboard + another projector in synergy) but gives you a slight idea of how the class went. And you can see the worksheet here: Zombies and Logistic Growth but I’d probably change a lot of it now 🙂
