Flashy animations are all the rage on cable news networks.  And people love infographics.  Both show a illogical love for graphs made out of circles.

From the NYtimes.com : http://www.nytimes.com/interactive/2012/02/13/us/politics/2013-budget-proposal-graphic.html?hp

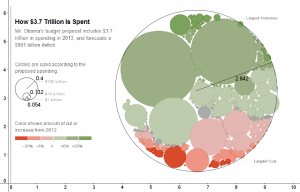
radii measured with geogebra after constructing a circle through three points plotted on the edges of the graphics circles.

There are two issues: squared ratios, and packing.

The first arises that as you change the radius of the circle, the area will increase by the square of the radius.  So the designer has to choose one measurement to represent their unit.  It appears that they chose area for this graph.  The given scale seems accurate for the $100 billion circle’s area to the $10 billion circle’s area.  However, the $1 billion circle appears to be off, or I can’t measure it precisely enough.  The problem here is that we are better at recognizing linear relationships rather than square relationships.

The problem here is human intuition.  Does the largest circle look like 10 times as large as the medium one?

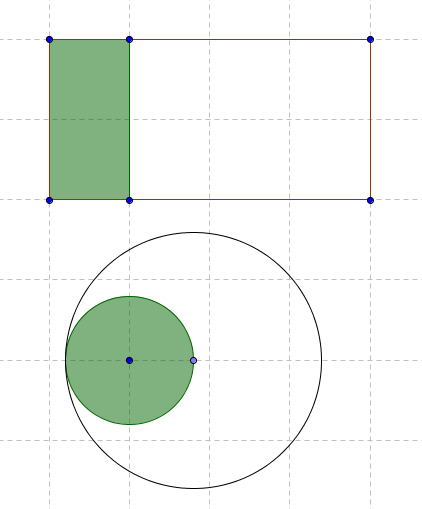
Consider these two representations of an area growing by a factor of 4.  Which is more natural?

To the unpracticed geometer, it may seem very difficult to believe four green circles fit into the large one.  Large area-scaled circles “seem smaller” than they should

That is the second issue: packing.  Rectangles are easy to pack.  Copy that green rectangle 3 more times and it will fit exactly in the area outlined.  But to fit the circle into its large circle of 4x the area, it requires distortions.  Those distortions harm the communication of knowledge.  Back in the first image, they attempt to pack a lot of various budget area’d circles in a large circle.  But the empty space makes the budget cover an area much larger than it should.

Infographics should always aim to present data in a way that makes it easier for the public to understand.  When style is chosen over substance, the information is distorted, literally.  Because of the competing effects of being too large or too small, I don’t believe the mis-communication was malicious.  Rather, it was ignorant.

Dan Meyer has morphed his “What can you do with this” edu-meme into “#101qs”:  what questions pop into your head upon observing a picture, movie, or other demonstration.  The more likely it is that a student will ask that question, the better.

I will present one now.  For your consideration,

“13 Folds”

If you tossed that up in your class, what would the kids say?  What’s the first question that pops into your head?

I’ll offer my own thoughts, and I welcome you to share yours in the comments.

I think this image has a lot of things going for it.  It is clearly the ACT1 image.  Toss it up.  Don’t say anything.  What will the kids ask?

What is it?
Toilet Paper.
That’s hella toilet paper!  (excuse the norcal slang 😉 )
yeah!  it’s a lot!
How much?
I dunno.
What do you mean you don’t know!? you’re the teacher!
Can we figure it out?

At this point, you can go to ACT2:  Have the students figure out what they need.  In this case, there’s a rather nice ACT2 image:

Act 2

Alternatively, you could say 5 feet by 2.5 feet on the image.  Or if you’re really brave, you could estimate it by the heights of the kids in the screenshot.  Ideally, you don’t have to say much else.  To a stuck student I might offer only: “unfold it“.

Extensions:

1. Graph it.
2. How many rolls did they buy?  What did it cost them?
3. How thick is the paper?  Graph THAT.
4. How many layers are at the 13th fold?  Another graph to make!
5. Why toilet paper?
6. What is preventing the 14th fold?  Why did they stop?

And finally,

Act 3

Ah, but there’s a bonus:  we have the actual video of them doing the folds.  What a great way to end the class!

http://www.youtube.com/watch?v=vPFnIotfkXo

Why toilet paper?  Try the Mythbusters episode: http://www.youtube.com/watch?v=kRAEBbotuIE

And then for those super interested kids who can access the final extension questions, you can lead them through Brittany Gallivan’s solution for arbitrary paper: http://en.wikipedia.org/wiki/Britney_Gallivan

Credit to Dr. James Tanton http://www.jamestanton.com/ for leading the actual exercise at MIT.

Toss me some comments!

In brainstorming about opposites and the additive inverse, I came up with an idea about justifying one step equations with this displaced water video.  But, it doesn’t quite lend itself to subtracting from both sides.  I’m going to try this as is, and perhaps we can come up with ideas in class about how well this lends itself to x+800=____ish.

I think this could also take a geometry route.  It reminds me of the demonstrations that a cylinder of height 2h and radius h has equal volume to (a sphere of radius h + a cone of height and radius h).

But right now, the ideas are in their infancy.

P.S. what did you get?  Here is the answer.

In the style of Dan Meyer’s WCYDWT… I may not have time to do a full lesson around this in my Algebra class.  There are only 4 days left and we are rushing through  the required tests.  But inspiration hit me when I saw this view:

I

Click for video

I put it up in my small 6th period class to get a taste for  how things would go.  Students immediately related to it (one kid correctly named the BART station) With a little prodding — “did you see the guy with the bike who was bookin’ it?” — they talked about how fast people were going.  Then they talked about trying to go down an escalator going up or up and escalator going down.  We didn’t get to any sort of problem solving, but we did count that it took about 30 seconds to merely ride the escalator up.

More on this as it develops… especially if I have time to implement it fully.

The Holt Geometry book starts every section with some “real world” application of the topic.

Its a bad book.

EDIT: I’ll revise my comments from earlier this year.  Its an OK book.  In writing classes a common piece of advice is “show, don’t tell.”  The Holt Geometry book, along with many others, fail in this regard.  It does nothing for a student to read in chapter 1 that a^2+b^2=c^2.  The Pythagorean theorem is a result of a long logical flow of geometric arguments.  (and still, the inane “Who uses this?” motivators make me want to defenestrate somebody) -2010.05.04

I just used a mathlet I found online: “Triangles By Side” (source: Math Hombre) in a lesson for geometry. (uploaded here: http://scottfarrar.googlepages.com/geom2009 The worksheet http://scottfarrar.googlepages.com/TriangleCategories.pdf ) It worked very well.

A few notes:
0. This was our second day on triangles so I had not used the vocab for each category. I purposely left it to the end of class then we all labeled each category as a class. Students worked in pairs, 1 computer per pair.
1. Students were a little confused about starting with the scalene. There’s not much to “observe” there. I think the best one to start with is the isosceles.
2. Its kind of a shame that the 3,4,5 and 6,8,10 are the only right triangles possible. Next time I would bump the sliders up to 13 so that students could make a 5,12,13. (obviously we haven’t covered pythagorean, but students were able to find the triangles easily enough)
3. I actually didn’t have the 2nd mathlet up there when my students did it. They used the first one for both activities.
Pros: integer lengths for c are easy to list. Students had no trouble figuring out what to do.
Cons: students don’t automatically consider fractional side lengths for side c.
This can be a pro, however!! A kid says if a=4 and b=6, c can be 3, 4, 5, 6, 7, 8, 9. Then they are ripe for me to ask “can c be 2 and a half?” They can flip back and forth from c=2 and c=3 to guess at what c=2.5 looks like. Then I ask “can c=2.1? 2.01? 2.001?” It was great to have students interrupt me half-annoyed and say “As long as its more than 2, its ok“

The one I just made (the 2nd one for 10-30) might be “too helpful” for day 2 of triangles. This is probably better as a review or lecture demonstration. http://scottfarrar.googlepages.com/triangleineq.html

So I think I might change my worksheet back to using the first mathlet, or a modifed version of the first. I’d limit the way they interact with side c first. Then I can give them more freedom to explore rational side lengths.

I welcome feedback and suggestions!

http://scottfarrar.googlepages.com/circumcenter_lomaprieta.html

So I put together this mathlet in anticipation of doing Triangle Centers. I love it, and I hate it. On one side, I’m very satisfied with how it turned out implementation-wise. On the other side, I’m not satisfied with what the lesson is. This is not a 50 minute activity. So they find Loma Prieta. Big whoop! There’s not really a *problem* to solve.

Could I muddy up the data? Could I muddy the data? Or should I go and try to get actual USGS data in terms of when the first shockwaves were felt and where. With all the differing topography in the Bay Area, I’m sure the shockwaves were not perfectly circular. And yet, if we took a lot of data we could probably do the calculations/constructions needed in order to find a good estimate for Loma Prieta.

Whats frustrating is that this lesson is not ready, and I’m not sure if I’ll have time to get it all the way there by the time this comes up in the year.

I did this with my students about a week ago: http://scottfarrar.googlepages.com/geom2009

Previous Knowledge: students have copied and bisected angles and segments before “IRL” using compasses and straightedges.

It went very well for a “first time” on computers this year. The versions of the files I initially used did not limit their tools, but I have now changed the mathlets: you are limited to Euclidean constructions via compass, straightedge and points/intersections.

The fourth mathlet is too hard. The first three took most of my students about 20-40 minutes to get through. So I definitely need a fourth problem that is relatively simple, yet exposes them to something new in Geogebra.

“Free exploration time” works for some students, but if they are that interested, they can do it at home on their own computers. I’d rather have an engaging mathlet.