Evaluative Listening and Khan Academy
Dylan Wiliam writes about teachers listening to student responses,
When teachers listen to student responses, many focus more on the correctness of the answers than what they can learn about the student’s understanding (Even & Tirosh, 1995; Heid, Blume, Zbiek, & Edwards, 1999). It is easy to identify such teachers because when they get incorrect answers from students, they respond by saying things like, “Almost,” “Close,” or “Nearly; try again.” What the teacher is really saying is, “Give me the correct answer so that I can get on with the rest of my script for the lesson.” Brent Davis (1997) called such teacher behavior “evaluative listening.” Teachers who listen evaluatively to their students’ answers learn only whether their students know what they want them to know. If the students cannot answer correctly, then the teachers learn only that the students didn’t get it and that they need to teach the material again, only, presumably, better. (emphasis mine) (Chapter 4, Kindle Locations 1761-1768). Wiliam, D. (2002). Embedded formative assessment. Solution Tree Press.
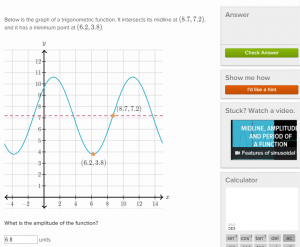
Consider how similar that is to Khan Academy’s current capabilities of assessment. If KA only collects the student response and evaluates it as binary correct or not– then KA only learns that the student didn’t get it and offers to reteach it (with a video) or give a hint. Furthermore, both the video and the hint are non-personalized since they do not account for what the student’s input was.
Wiliam distinguishes a separate type of listening: interpretive.
“What can I learn about the students’ thinking by attending carefully to what they say?”
Can Khan Academy do interpretive listening? Can technology in general do this? Dynamic Math Software like Geogebra or Desmos might interpret your input by attempting to incorporate it into the model it is presenting–but is that listening? Try an example:
I see it as much more valuable feedback than what KA offers, since the Geogebra feedback contains more information. A response like 6.8 now shows that what you have entered does not match the blue function. However it is still not as flexible as a human teacher, that could not only interpret the narrow numerical responses but also take an input like “why do we measure amplitude from the midline?” nimbly. KA offers a video on the subject but you’ll have to go looking for the answer to a specific question.
Of course, a teacher might be best served by a combination of Geogebra and their own human capaiblities. A geogebra applet set up ahead of time anticipating certain responses can aid the teacher in the dialogue with students. The computer can graph accurately, instantaneously, repetitively, and in parallel (multiple users at once). The teacher can use Geogebra to augment their own interpretive listening and augment the information feedback to the students. The KA question here does not augment; its listening is solely evaulative and its feedback is non-personalized and non-specific. A teacher using this KA lesson does not teach more efficiently: either the teacher abandons the student to the software’s help or the teacher supplants the software’s help by helping themselves. In either case, the teacher and KA have a substitute relationship not symbiotic relationship.