Golden’s Rings and Polyhedral “Cups”
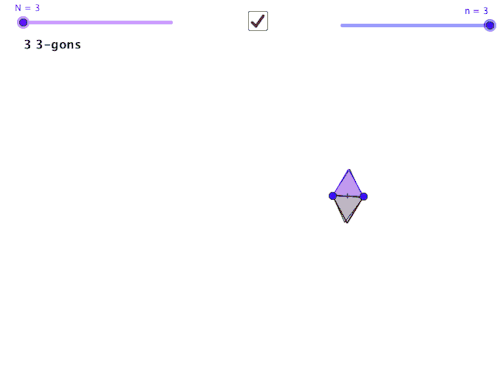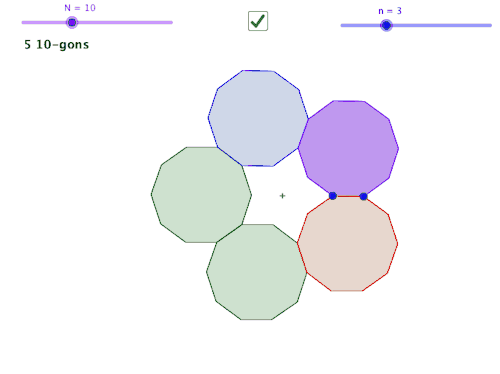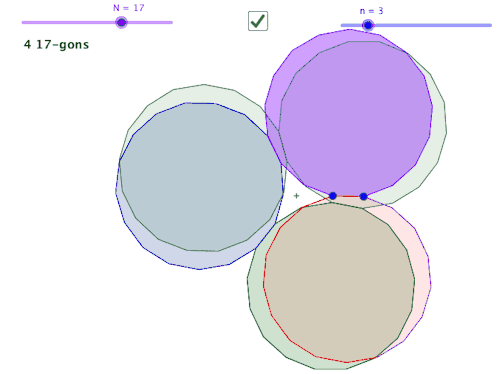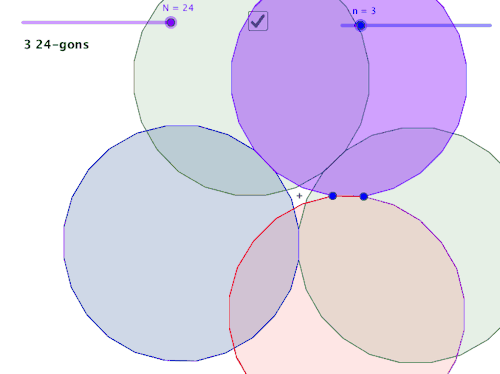
John Golden @mathhombre just posted some very interesting GeoGebra files exploring polygons repeatedly constructed on an edge of the previous. Here’s his post.
The sweet spots between # of sides of the polygon and the # of sides to offset for the new construction reminds me of the platonic solid and polyhedron lesson I do for Geometry.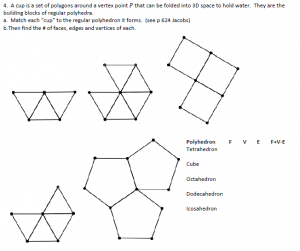
Instead of giving students the whole net, we would explore which regular polygons can be systematically repeated around a vertex and then “bend up into 3D space” in a manner that would “hold water.”
So, considering 2 triangles… no they just fold up on top of each other. But three triangles fold up into a nice tetrahedron “cup” (missing its cap)
Four triangles? Fold them and you see a square base missing– but fold another four and you get the tetrahedron. The idea being that we should do the least complicated instructions to find these shapes. If the “instructions” are short then perhaps they are more likely to occur in nature, especially if you are lacking storage space in your DNA/RNA.
and you get the tetrahedron. The idea being that we should do the least complicated instructions to find these shapes. If the “instructions” are short then perhaps they are more likely to occur in nature, especially if you are lacking storage space in your DNA/RNA.
So which polygons actually form repeatable cases? The ones that can repeat around a vertex and leave a gap. Spoilers: three, four, five triangles, three squares, three pentagons. These correspond to the five platonic solids. There are some interesting differences however between the icosahedron’s repetition of its “cup” compared to the others. And consider the difference between the tetrahedron needing just one more triangle vs. the octahedron, dodecahedron, and cube needing full repetitions of their cups.
This can also be taken to extending/linking the concepts of tiling and polyhedrons. Two triangles and six triangles don’t fold up into a cup but they tile the plane instead. Are Regular Polyhedrons “closed tilings” of 3D space? #continuummath ! 🙂
See one of my PDFs for the students here.
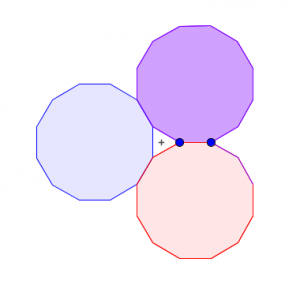 So… back to John Golden’s geogebra file. I wonder if there are links to different types of polyhedra from the rings he’s created. Do repetitions of this dodecagon with a triangular gap form a polyhedron? No, but it does tile. So how about some of John’s other combinations?
So… back to John Golden’s geogebra file. I wonder if there are links to different types of polyhedra from the rings he’s created. Do repetitions of this dodecagon with a triangular gap form a polyhedron? No, but it does tile. So how about some of John’s other combinations?