Prove that two triangles are congruent. Sometimes seen as the “first real proofs” of a Geometry course (but they should probably not be the first proofs done, and the types usually done aren’t much of proofs– but let that be for now).
How do you get students to feel the need to prove? How do we give them a reasonable headache alleviated by the learning target’s aspirin?
The headache-aspirin idea can be illustrated like this: add the first 100 integers. 1+2+3+…+100. The headache is that it seems like a lot of tedious work, but using Gauss’ arithmetic series folding idea, we fold the long sum onto itself and add pairs inward: 1+100, 2+99, … getting 50 sums each equal to 101, thus finding the sum of integers from 1 to 100 is 5050. This legend is oft repeated as Gauss’ clever way to get around a teacher’s tedious punishment: notice how even in legend we appreciate the origin of a clever idea as a way to reduce tedium.
Back to triangle proofs. We want students to see SSS, SAS, ASA, HL (SS-rightA) as useful tools to show that two triangles are congruent. Dan Meyer made an astute comment: If proofs are the aspirin, the doubt is the headache. The congruency shortcuts are very abstract, but furthermore, a student may not have reason to believe or disbelieve whatever you are going to say on the subject of congruecy. Two threads emerge here:
(1) why do we want to show triangles congruent? How can we make a student doubt that triangles may be congruent?
Triangle congruence is our tool of two dimensional congruence. So we need to have students care about congruence in general. If your students are philosophical (and many are) then studying the idea of sameness/congruency has some grounding there. But all students are going to want something concrete as well.
(2) why do we use these little 3 part shortcuts?
The accepted shortcuts are an efficient result. Nothing wrong with showing triangles are congruent by matching all six parts: SASASA — nothing wrong except efficiency. Arriving at the result of the triangle congruency shortcuts can be done by students themselves.
So here’s my scratchwork for a lesson idea: work from the opposite case, can we make a student doubt that different triangles exist? Building Different Triangles We infuse doubt by assigning students to find non-congruent triangles. When they run up against their sandbox’s boundary– the conditions that cause some triangles to be automatically congruent– they can all of a sudden doubt that triangles can always be made differently.
Students in groups are given the task to build different triangles than their groupmates, given a set of matching triangle parts. The given parts are either physical manipulatives or digital (advantages with each one)
0. Do we agree that if three sides and three angles are given to us, we can make only one triangle? Why or why not?
0.5 Think ahead, what if we are given only 5 parts, can we make two different triangles? What about given other numbers of parts, like 2? Can we make different triangles then? How many different triangles?
1. Given A=30, AB=3, BC=2. Make as many different triangles as possible. Related concept: SAS, Law of Cosines eventually. Geogebra interactive.

Geogebra applet exploring Angle Side Side
2. Given AB=3, BC=2. Make as many different triangles as possible. Related concept: triangle inequality. Geogebra interactive.
3. Given AB=5, BC = 4, CA = 2. Make as many different triangles as possible. Related concept: converse of Pythagorean theorem. Geogebra Interactive.
4. Given A=40, B=30, AB=5. Make as many different triangles as possible.
5. Given A=40, B=30, BC=5. Make as many different triangles as possible.
6. Given A=53, B=57, BC=5.35, AC=5.1. Make as many different triangles as possible.
Be careful with the chosen values. Sometimes (especially the first one) you want the students to arrive at different triangles. Save the “we can’t!”/”they’re all the same” moment (SSS (3) / AASS (6) ) for later in the progression.
 We also don’t need to restrict ourselves to tech-based manipulatives. Straws and string work great for the SSS case.
We also don’t need to restrict ourselves to tech-based manipulatives. Straws and string work great for the SSS case.
What kind of conjectures would students make when exposed to this kind of task? Many will apply the triangle angle sum, or have it solidified in their mind: meaning they can conjecture we at most need to be given two angles. Hey, that’s a proposition we can prove! That’s one students can prove, or at least justify. And its not arbitrary or needless: its something that is a significant step towards reducing tedium of triangle differentiation. If we know two angles, we know the third.
And how about conjecturing and proving statements like: to show two triangles are congruent, at least three parts must be known. (note, hypotenuse-leg gives three parts: two sides and the right angle) Or, at least one side must be known. These are within the grasp of proof by the students because they will have had the experience of seeing the counter examples and of building intuition about what forces the known congruency shortcuts to be what they are.
Thoughts? extensions?
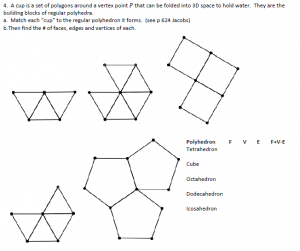
 and you get the tetrahedron. The idea being that we should do the least complicated instructions to find these shapes. If the “instructions” are short then perhaps they are more likely to occur in nature, especially if you are lacking storage space in your DNA/RNA.
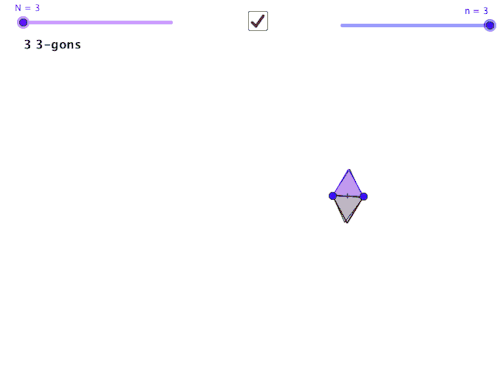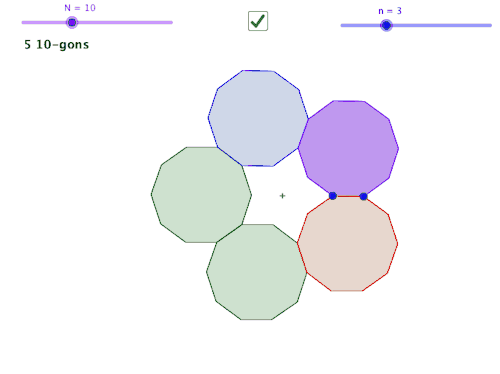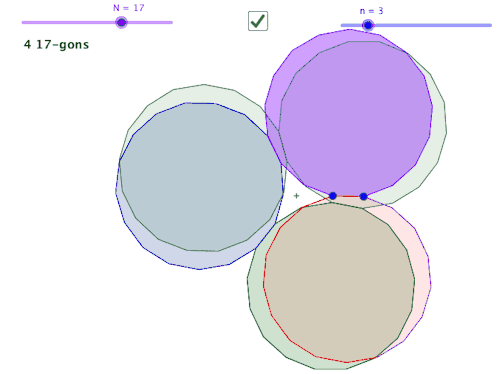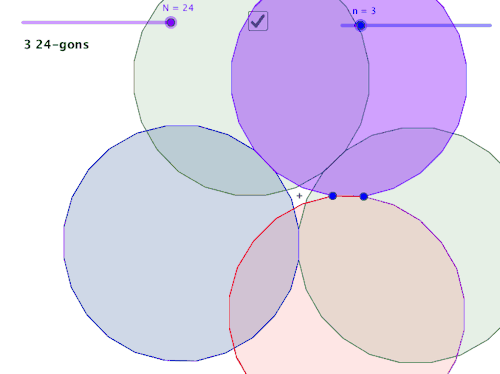
and you get the tetrahedron. The idea being that we should do the least complicated instructions to find these shapes. If the “instructions” are short then perhaps they are more likely to occur in nature, especially if you are lacking storage space in your DNA/RNA.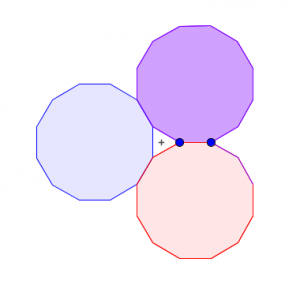 So… back to John Golden’s geogebra file. I wonder if there are links to different types of polyhedra from the rings he’s created. Do repetitions of this dodecagon with a triangular gap form a polyhedron? No, but it does tile. So how about some of John’s other combinations?
So… back to John Golden’s geogebra file. I wonder if there are links to different types of polyhedra from the rings he’s created. Do repetitions of this dodecagon with a triangular gap form a polyhedron? No, but it does tile. So how about some of John’s other combinations?

 We also don’t need to restrict ourselves to tech-based manipulatives.
We also don’t need to restrict ourselves to tech-based manipulatives.