Marilyn Burns (@mburnsmath) recently blogged about a problem she came across via NCTM’s Teaching Children Mathematics and Mike Flynn

 

I’m looking for some Ts to try out my @TCM_at_NCTM task w/ their students & share their work. Thanks! #ElemMathChat pic.twitter.com/4ytSf9DtAS

— Mike Flynn (@MikeFlynn55) August 15, 2016

This Bike Shop Lesson ended up being rich not just for the students, but also for herself. In exploring the underlying structure, you can touch on many different topics. See Marilyn’s blog, Henri Picciotto’s blog, and Simon Gregg’s tweets for a more there!

 

---

As I read these thoughts from others it reminded me of a similar lesson I did with high school Algebra 2 students. It also dealt with partitions of numbers, but exploring different constraints than the unicycles, bicycles, and tricycles. In exploring those constraints, my students found some interesting patterns including Pascal’s Triangle, powers of two, the Fibonacci sequence,

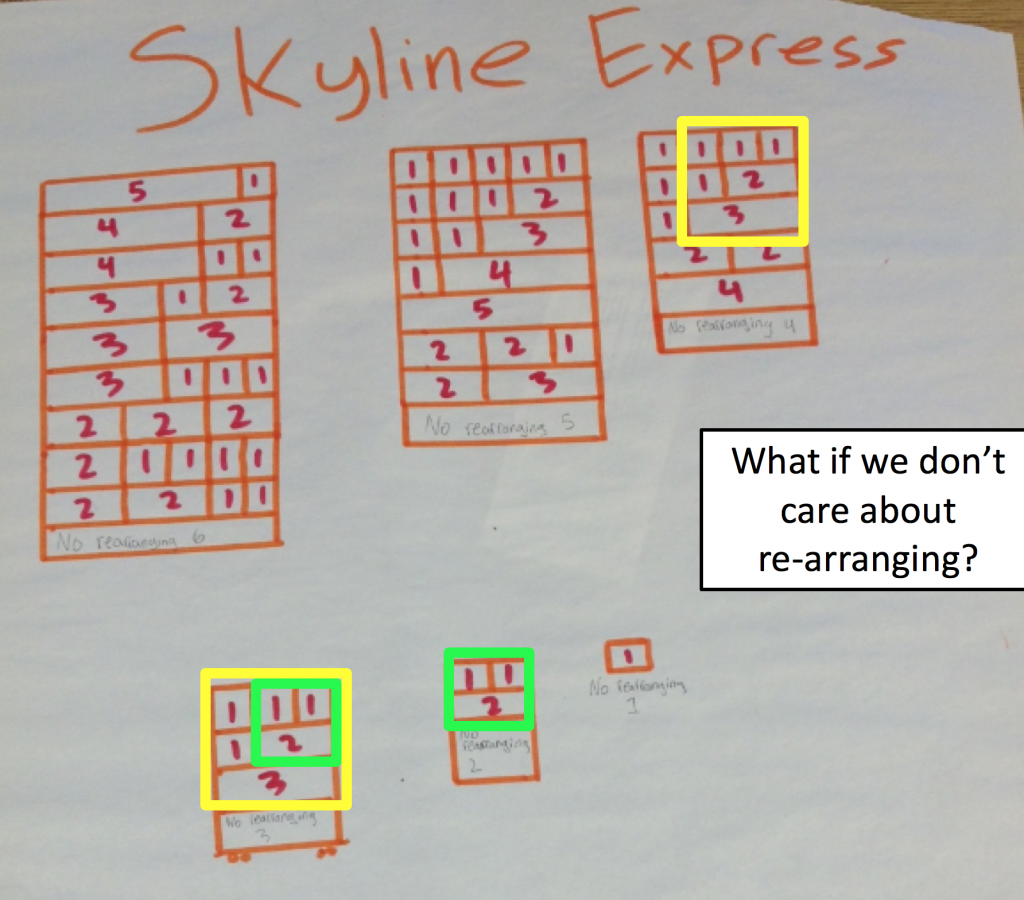
Traincar Number Lesson

Here are three trains with length 6, but they are made up of different numbers of cars and types of cars. How many different trains are there?

I purposely left the question vague because I wanted students to interpret it in a variety of ways. Influenced by Yackel and Cobb’s 1996 article, “Sociomathematical Norms,” I wanted students to develop their own agreements in their groups about what counted as different.

[note: I did explicitly ask my students about trains of length 5 to start them off. I may choose otherwise in the future]

Students refine the question

I gave the students cutouts (included in PDF) to support a few aspects of problem solving. First, the scaled cutouts support non-numeric representations. Second, the easy-to-change nature means students can re-arrange the blocks quickly and are not locked to what they have first represented. Third, they must formalize thinking from the cutouts to more permanent representations. And finally, the cutouts are easily worked by more than one person so it can promote discussion in a group.

Here are some of the thoughts my students had:

1. Is 2+2+1 different than 2+1+2 ? What if they’re the same?
2. What if you don’t allow copies of a car? (so 2+2+1 is not allowed because there are two “2s”)
3. Are all “1 cars” the same?
4. Can we use negative cars? (like a car of length “-2” for example)
5. Can we use partial cars? (“1.5”)
6. Are reflected trains the same? (2+2+1 and 1+2+2 might be the same, while 2+1+2 is different)
7. what if we are limited by how many cars? (only allowed to use exactly three cars, for example)

I was very impressed by how much the students embraced the chance to question the rules and develop their own. Its something we teachers should do more often! I expected to see questions 1 and 6 from the students, but the other questions each surprised me in some way. I learned a lot about what my students could do when given the chance. They revealed a lot of thoughts they had about permutations, combinations, sorting, number, structure… I was able to grab onto this knowledge later in the year as we formally talked about those subjects.

The freedom of exploration in the problem let students from multiple ability levels contribute. One student who was struggling was the one asking about negative car sizes. Its the kind of question that makes you pause; you may wonder if he’s asking about this does he understand the problem? I am very glad I let him explore it with his group. The answer, “infinite number of trains!” is much more meaningful when the student discovers it, rather than the teacher disallowing the investigation by providing the answer.

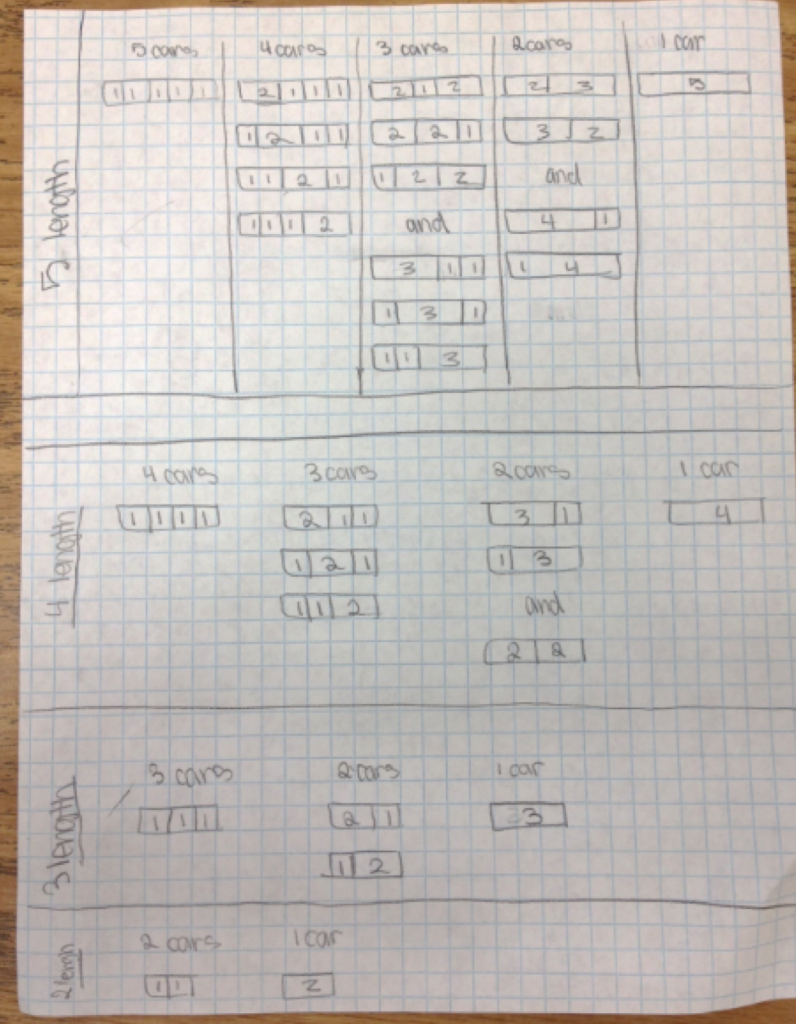
Student work

Also, I was able to let the students experience the results of testing their own conjectures. Here are some results of their investigations: (there are some small errors in their work)

1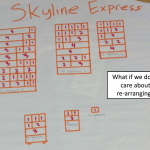	3
4	7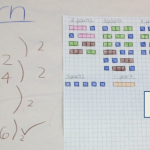

Most groups found the pattern that with certain assumptions, the number of trains of length N is 2^N. But the exposure to other assumptions generating other patterns was a great place for a meta-discussion about mathematical practice, and the hidden structure of numbers.

We discussed how some groups patterns fit together and how as a class we explored a lot of boundaries to the problem. We talked then about some of the boundaries we did not explore: such as limitations to only certain lengths of cars. (Notice the limitation to 1s, 2s, and 3s cars is the Cycling Shop Problem!

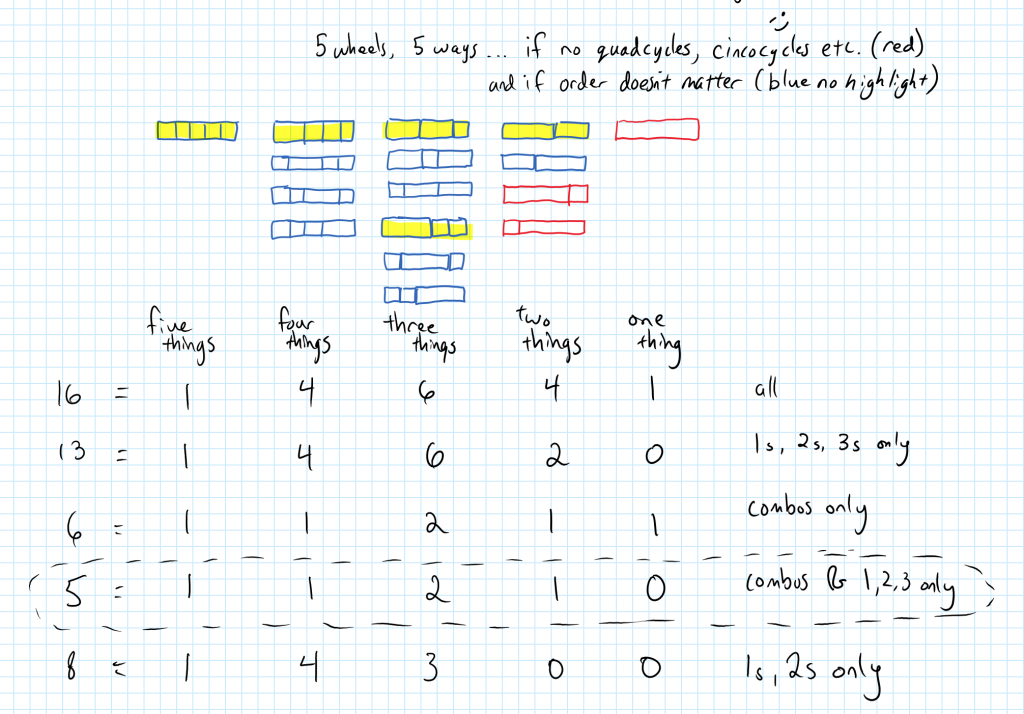So when Marilyn and Henri were sharing ideas about the cycling shop problem I recalled my students work and how we were linking the various assumptions made into a larger structure. I played with thinking about the unicycles, bicycles and tricycles built from 8 wheels inside the organization of combinations and partitions.

How fun was it to come back to this problem myself and dig around for new concepts! And its not nearly done…

Limiting to only 1s and 2s has another fun result that I wont spoil here… try it yourself! try it with your students!) Another extension is to limit to prime length cars only. I concluded with sharing the Goldbach Conjecture:

Every even integer greater than 2 can be expressed as the sum of two primes

I asked my students what they thought, how they might approach it, how its connected to the traincars they’ve thought about. Then I let them know that the problem is unsolved. “You are part of the community of mathematicians… testing assumptions, making conjectures, organizing and sharing ideas.” It was one of my favorite lessons I’ve done. (Also a great way to lead into winter break… “Your HW for break is to solve Goldbach, have fun!”)

Traincar Lesson PDF – this is ‘localized’ with a playful name for my school and timing in the year (“Skyline Express”) but also I gave it as a participation quiz, so some of the introduction of the task in this pdf is specific to that classroom format.

Differentiation to all levels

Notice aspects of these partition problems have piqued curiosity of students from elementary school, to high school, to teachers, and of course to professional mathematicians. When the learner has a chance to refine the question for themselves and explore their own ideas, the task is becomes personalized. And when the tasks are personalized then we can make them socialized: people sharing their own ideas and work.

---

References

Skyline Express Lesson Materials PDF – Scott Farrar 2013

NCTM – Teaching Children Mathematics – The Cycling Shop http://www.nctm.org/Publications/Teaching-Children-Mathematics/2016/Vol23/Issue1/The-cycling-shop/ August 2016

Yackel, E., & Cobb, P. (1996). Sociomathematical Norms, Argumentation, and Autonomy in Mathematics.Journal for Research in Mathematics Education, 27(4), 458-477. doi:1. Retrieved from http://www.jstor.org/stable/749877 doi:1

Earlier today I was in a discussion with @mathhombre on Twitter about what is needed in an College Algebra course (roughly equivalent to Alg2+Precalc for high school).  I came to the (perhaps too radical) idea that lines are simulateously one of the most applicable concepts to a person’s “real life” but also one of the most useful tools for accessing higher math.  There are entire areas of study about linearization as a tool to simplify complicated cases not just in pure math, but economics, physics, engineering, etc.

Any that is just the prelude.  If we are going to talk about lines, what happens to the darling of any high school level algebra course?The quadratic function / The parabola.  Consider f(x) = x^2 – 2x – 15.  Factoring, we obtain f(x) = (x+3)(x-5).  A subtle idea that might be skipped over: f(x) is the product of two lines.  Literally lines y = x + 3 and y = x + 5.  Do our strudents face the idea that a linear factor and a line are the same?  Consider the product of the values of the lines — point by point.  Try it with Geogebra.  The f(3) = (line1 at 3)*(line2 at 3) = (6)(-2) = -12.

We also know the Fundamental Theorem of Algebra will guarantee n roots for a degree n polynomial.  But those n roots may have non-real parts, for example g(x)=x^2 + 4 does not factor over the reals  g(x) = (x+2i)(x-2i)

So can our “line*line” idea survive these new types of models?  And where can we see these complex lines?  The product relationship still holds.  g(3) = (3+2i)(3-2i) because the imaginary terms will cancel since complex roots always come in conjugate pairs.  g(3) = 3*3 + 3*2i + 3*-2i + – 2i*2i = 9 + 4 = 13.  But wait, lets slow down.  3 + 2i is a point.  A point on the line x+2i.  It is a line hidden to our view because we lack the dimensions on our plane to see it.  We have only the 1D real line as our inputs.

So lets consider the imaginary part of our domain.  Click the picture to see a larger view:

That’s g(x) = x^2 + 4.  The red axis is the standard x-axis.  The green axis is the standard y-axis.  But the blue axis represents the imaginary part of our domain.  A normal classroom might be used to plotting 3+2i on a plane, but do we often make note that its a nominally different plane than the one we graph functions upon?  3+2i will be on the plane that passes through the red and blue axes.  I chose to view it this way to keep y outputs as close as possible to our usual view.

Ok so lets see 3+2i and 3-2i and their output product 13.  I included two views here since it is difficult to get a grasp of the 3D situation.

These lines y = x+ 2i and y = x – 2i are kind of abuses of notation.  They should be specified that they are lines in space, namely y=x limited to the level planes Im = 2 and Im = -2.

There’s certainly more to do with exploring this idea, especially making the presentation more robust.

What really appeals to me is the symmetry of a quadratic’s complex conjugate roots is similar to the symmetry of a separate quadratic’s real factors around the axis of symmetry.  Even more, the idea of the imaginary number i as a 90 degree rotation fits puzzle pieces together.  The complex roots are 90 degree rotations around the axis of symmetry of a reflection of the parabola (reflect across a horizontal line passing through the vertex).  This is the part that holds some promise, but that I haven’t quite explained in my own head yet.

I invite you to play around with the Geogebra applet I used to explore this.  It is set up to start with x^2 – 8x +18.  Find the complex roots algebraically first, then see if it meshes with the visuals in the applet. Thoughts?

@ddmeyer appeal to coins already an attempt at “real”/accsble . But strange constraints to know. Scrap&Stepback: 2eq2var: Whats intrstng?hmm

— Scott Farrar (@farrarscott) October 15, 2014

Dan Meyer posted a classic example of a “coin problem” the other day on Twitter.  The problem was in Pearson’s Common Core Algebra 2 text.  Lets assume positive intent from Pearson’s authors in their choice of inclusion here, since at first glance, it may not seem very “common corey”.  But actually, regardless of their intent, lets see where this kind of problem has (1) traditionally taken us and (2) what we can do with it to explore non-traditional approaches.

This post is adapted from my comments in Dan’s thread.

Mark has 42 coins consisting of dimes and quarters. The total value of his coins is $6. How many of each type of coin does he have? Show all your work and explain what method you used to solve the problem.

What kind of problem is this?  Usually this comes up during a systems of linear equations unit in an Algebra 1 class.  The text itself is an Algebra 2 book, so we’re probably safe to assume their intent is to use it as an example of a slightly dressed up system of lines exercise.

So my thoughts are to step back a little bit.  (1) its 2 equations and 2 unknowns — what is interesting and important about those?  What kind of mathematical structure is this?  (2) What does the context of coins do to our structure?  (3) Does the coin context add to our ability to uncover the underlying structure?

Intro

Consider its a little strange to know how many coins you have but not how many of each denomination.  An initial sign of contrived context that students pick up on.  Mostly by high school, students have formed some identities in the classroom that oblige them to cooperate with teacher instruction, so if they’re not initially interested, they may hang with you a little bit. But perhaps some loudmouth in your class will point out some of the strangeness of the contrived situation. #embracetheloudmouth

So perhaps at some point during the lesson series you then have the opportunity to say, “you’re totally right, Lou D’mouth, in what situation could we know the number of coins total and their value total, but not their partition?”

This is where you can set up the class to turn this coin problem on its head, as it were.  (rimshot!)

Letting the kids “get meta”

I like Denise Gaskins’s @letsplaymath idea:   Turn it into a 20-questions game: Stu reach into coin jar & grab handful, others ask Qs to find out what coins they have.?

This changes the requirements of the task: not only do we want to find a solution but we care ostensibly about how efficiently we can do it with respect to the number of questions asked.  Why does it take at least two questions?  Denise’s activity might not go on very long but that’s fine because why will the students stop doing it? They’ll figure out how easy it is!  They’ll wrap their heads around it.  Maybe the teacher can explicitly challenge groups to try to ask a single question to answer # of quarters and # of dimes.

(Presumably, we’re going to disallow “how many quarters?” although its still interesting that we still need two questions there…)

Furthering this section could be questions like:
Q.  If you ask “how many quarters?” and they respond “8” then why does that not let us know how many coins are in their hand?

Expand on the Structure

Now we can acknowledge the contrivance because its going to lead us to something special about this mathematical structure. We acknowledge and loosen our contrivance: parameterize the # of coins.  A number of people on twitter responding to Dan had this idea in addition to myself.

(Lets make the numbers smaller) Say we have $2.00 If we only use quarters and pennies… how many coins do we need? N=8 coins (8q0p) is one way… N=104 is another (ask how!).

1. spend some time finding Ns. mathematical practice standard: make use of structure! (How do we know when we’re done?)

2. To add up to $2.00 does every N (coin total) break down into only one quarter and penny partition? why?

3. Why do some Ns (105 e.g.) not have any solutions?

4. ***What is it about the quarters and pennies, Ns, and $ totals that forces us to have unique solutions or not?***

and 5. Can we contrive a coin-situation so that there are $s,Ns with multiple quarter-penny partitions? Is this possible?

Think back to when you were a student

I remember a lot of handwaving and “worship” in my own education towards the fact that 2 equations and 2 unknowns has a solution. (and 3 eq, 3 unknowns, etc…)

But statements like “ok so this is 2 equations and 2 unknowns so we know how to do it” are exactly what contribute to the magic spellbook idea of math. Kids feel that those who are good at math know the right spells to incant, and “2 equations 2 unknowns” must be a pretty good spell if it makes answers appear out of nowhere!

Don’t solve too quickly

I think this would be a rare case in which I would NOT go for a graph quickly. Yeah, we know about intersections of lines. Yeah we can show these coin relationships are linear.

But can we justify to ourselves that this idea of limited solutions based upon # of constraints is generalizable? We start with quarters pennies sure. In the middle maybe we prove something about # of solutions of systems and we talk about other ideas like mixtures and such. But by the end? We need students to grok (http://en.wikipedia.org/wiki/Grok) this idea of systems and solutions.

Descartes before dehorse

Maybe this is something that the teacher holds in his or her head.  But the deeper and richer the teacher is thinking about the mathematical structure, the more links and hooks and connections can be made between student ideas.  Here we might think about the genius of the Cartesian plane a little bit:

The graph informs us of:

– the infinite nature of the linear models
– the monotonic nature of the linear models
– the difference in ratios between coinA:coinB and valueA:valueB (thus different slopes)
– all of the ordered pairs that fit the conditions of the coin count
– all of the ordered pairs that fit the conditions of the value total

And combining our geometric knowledge about lines at different angles, mapping that onto the linear models, mapping THAT onto the coin situations… that’s how we are justifying our singular solution.

How this all might play out in a classroom would be just that extra 15 seconds of wait time, that extra question for group discussion, that incremental food for thought…

Not so much that we want a full answer, but that we want the students to take up the role of justification.

T, to S: “Why DO we know there is one solution here…?”

Let the students bring it out into the discussion

And if S reasons via graph, great!

But S might say something like: “well if we take off a quarter, and add a time, we keep the coin total at 42, but lose value…. we’ll always lose value at this way so there can be no solutions with more quarters!”

That’s (a) proof by contradiction and (b) using concepts that apply for theory of functions: decreasing, monotonic. (in this case its a sequence) But also the S has synthesized a hypothetical that generalizes to a larger case: take off a quarter, add a dime. Then they’ve upped their abstraction by arguing that any case like that will not provide a solution. (And similar arguments can work for adding a quarter, subtracing a dime)

Then T has the opportunity to engage the class in a discussion of bridging the graphical and the deductive reasonings.

It may very well end up becoming a discussion on why Cartesian graphs are so great, and all the better! Lots of students struggle with graphing because they are stuck on procedure without realizing what a graph represents specifically in an instance, or generally.

Bouncing off the Literature

In the beginning of this post I brought up the idea that a student will go along with some ridiculous contrived situations because they feel obligated to conform to a certain identity in a math class.  I’m considering this in the context of Dr. Paul Cobb’s 2009 article regarding how students create, maintain and alter their identities during their education.  This can be a bad thing, as in the case study course:

The frustration and disenchantment that all the students voiced indicated that they were not identifying with mathematical activity as it was realized in this classroom but were instead merely cooperating with the teacher. (Cobb, 2009)

P., Gresalfi, M., & Hodge, L. L. (2009). An interpretive scheme for analyzing the identities that students develop in mathematics classrooms.Journal for Research in Mathematics Education, 40-68.

When thinking about classroom discussions, I enjoyed Walshaw and Anthony’s 2008 paper on classroom discussions.  A favorite quote:

Unless teachers make good sense of the mathematical ideas they hear in class, they will not develop the flexibility they need for spotting the golden opportunities and wise points of entry that they can use for moving students toward more sophisticated and mathematically grounded understandings. Reflecting on the spot and dealing with contested mathematical thinking demand sound teacher knowledge. Importantly, the way in which teachers manage multiple viewpoints is very much dependent on what they know and believe about mathematics and on what they understand about the teaching and learning of mathematics.

Walshaw, M., & Anthony, G. (2008). The Teacher’s Role in Classroom Discourse: A Review of Recent Research Into Mathematics Classrooms. Review of Educational Research, 78(3), 516–551.

Ran across this on reddit…

The smile inducing “how much does it cost?” is a great place to start.

But how about “how much area is wasted?” to touch on the packing problem of circles. http://en.wikipedia.org/wiki/Circle_packing_in_a_square

And hey, might as well kick it up into 3D… http://www.youtube.com/watch?v=uDJ3sor2oQ0

Dan Meyer has morphed his “What can you do with this” edu-meme into “#101qs”:  what questions pop into your head upon observing a picture, movie, or other demonstration.  The more likely it is that a student will ask that question, the better.

I will present one now.  For your consideration,

“13 Folds”

If you tossed that up in your class, what would the kids say?  What’s the first question that pops into your head?

I’ll offer my own thoughts, and I welcome you to share yours in the comments.

I think this image has a lot of things going for it.  It is clearly the ACT1 image.  Toss it up.  Don’t say anything.  What will the kids ask?

What is it?
Toilet Paper.
That’s hella toilet paper!  (excuse the norcal slang 😉 )
yeah!  it’s a lot!
How much?
I dunno.
What do you mean you don’t know!? you’re the teacher!
Can we figure it out?

At this point, you can go to ACT2:  Have the students figure out what they need.  In this case, there’s a rather nice ACT2 image:

Act 2

Alternatively, you could say 5 feet by 2.5 feet on the image.  Or if you’re really brave, you could estimate it by the heights of the kids in the screenshot.  Ideally, you don’t have to say much else.  To a stuck student I might offer only: “unfold it“.

Extensions:

1. Graph it.
2. How many rolls did they buy?  What did it cost them?
3. How thick is the paper?  Graph THAT.
4. How many layers are at the 13th fold?  Another graph to make!
5. Why toilet paper?
6. What is preventing the 14th fold?  Why did they stop?

And finally,

Act 3

Ah, but there’s a bonus:  we have the actual video of them doing the folds.  What a great way to end the class!

http://www.youtube.com/watch?v=vPFnIotfkXo

Why toilet paper?  Try the Mythbusters episode: http://www.youtube.com/watch?v=kRAEBbotuIE

And then for those super interested kids who can access the final extension questions, you can lead them through Brittany Gallivan’s solution for arbitrary paper: http://en.wikipedia.org/wiki/Britney_Gallivan

Credit to Dr. James Tanton http://www.jamestanton.com/ for leading the actual exercise at MIT.

Toss me some comments!

In brainstorming about opposites and the additive inverse, I came up with an idea about justifying one step equations with this displaced water video.  But, it doesn’t quite lend itself to subtracting from both sides.  I’m going to try this as is, and perhaps we can come up with ideas in class about how well this lends itself to x+800=____ish.

I think this could also take a geometry route.  It reminds me of the demonstrations that a cylinder of height 2h and radius h has equal volume to (a sphere of radius h + a cone of height and radius h).

But right now, the ideas are in their infancy.

P.S. what did you get?  Here is the answer.

In the style of Dan Meyer’s WCYDWT… I may not have time to do a full lesson around this in my Algebra class.  There are only 4 days left and we are rushing through  the required tests.  But inspiration hit me when I saw this view:

I put it up in my small 6th period class to get a taste for  how things would go.  Students immediately related to it (one kid correctly named the BART station) With a little prodding — “did you see the guy with the bike who was bookin’ it?” — they talked about how fast people were going.  Then they talked about trying to go down an escalator going up or up and escalator going down.  We didn’t get to any sort of problem solving, but we did count that it took about 30 seconds to merely ride the escalator up.

More on this as it develops… especially if I have time to implement it fully.

f(t): Help Me With Some Algebra

Given a chord AB and the intercepted arc S, is it possible to find radius r algebraically? (problem stated at f(t)) The consensus there seems to be no, due to the transcendental nature of sin(x).

But I find it interesting that r could be constructed with a compass and straightedge. However, I feel like I’m cheating with Geogebra since I had to place C in order to draw arc S. So I really wasn’t given S; I picked one based on C. Circular logic! (that’s a little math joke … ha ha ha.)

Update: http://www.mathforum.com/dr.math/faq/faq.circle.segment.html#1 Dr. Math has a nice page about solving circles given arbitrary parts. They reinforce the idea that this is a problem with numerical-only solution. Their solution involves Newton’s Method, something I myself am not very well versed in these days!